Wednesday, November 30, 2022
Dr. Nergis Mavalvala
Professor Cora Dvorkin
Professor Cora Dvorkin is a theoretical cosmologist at Harvard University. She was born and raised in Buenos Aires, Argentina, and received her Bachelor’s degree in Physics from the University of Buenos Aires. In 2011, she earned her Ph. D. in Physics from the University of Chicago and went on to pursue her postdoctoral research at Princeton University.
Professor Dvorkin has focused her studies on the beginnings of the universe, dark matter, and light relics. She investigates her research in Cosmic Microwave Background (the electromagnetic radiation that was left behind by “the first light”/early universe), the vast structure of the universe, and strong gravitational lensing (the distortion and magnification of light caused by the large gravitational field from the clusters of galaxies). With her research group, she has shown that – for the first time – machine learning techniques can accelerate the direct detection of dark matter disturbances. Her research group has also explored different dark matter scenarios using high-resolution simulations through precise statistical measurements of “dark matter substructure.” Recently, her research group used wavelet scattering transform (WST) – a way of improving image quality by stabilizing any rotations, translations, or deformations of data taken from galaxies – to perform the first field-level analysis of galaxy data retrieval. The use of WST by her team has shown to the astrophysics world the efficiency of it over traditional estimators and “black box” machines to obtain data of first galaxies.
With particle physicists, Professor Dvorkin identified a new production channel for dark matter produced through the “freeze-in mechanism” (which is the decay of photons in medium-massed plasma), which furthered her research in the strength of dark matter disturbances for detection in the universe.
Professor Dvorkin has been awarded prestigious recognitions in the scientific community, such as “2018 Scientist of the Year” by the Harvard Foundation for “Salient Contributions to Physics, Cosmology, and STEM Education” the 2019 DOE Early Career award, a Radcliffe Institute Fellowship for 2018-19, a Star Family Challenge prize for Promising Scientific Research in 2018 by Harvard University, and many more! Through her many research advancements and exploration of various methods to obtain data about the early cosmos and dark matter, Professor Cora Dvorkin has proven herself to be a magnificent contributor to the field of astrophysics and cosmology.
https://www.physics.harvard.edu/people/facpages/dvorkin
https://dvorkin.physics.harvard.edu/research-highlights/
Tuesday, November 29, 2022
Dr. Stephen Mayo
Dr. Stephen Mayo is a biologist and biophysicist at Caltech studying protein engineering. Before becoming a prominent researcher, Mayo studied Chemistry at Pennsylvania State University. Following his undergraduate studies, he went on to receive a Ph.D. from Caltech, where he currently works. Later, he was appointed to the National Academy of Sciences and the National Science board.
In his lab, Mayo is focused on developing a systematic protein design algorithm. This algorithm would be able to predict how proteins would fold based on their genetic sequence. Furthermore, Mayo aims to design proteins with enhanced or novel functions using this algorithm. Of course, this algorithm relies heavily on fundamental physics. For example, predicting how proteins will interact when they collide is as much a physical problem as it is a biological one.
Stephen Mayo's research is truly amazing as it shows how intertwined biology, chemistry, and physics are in our everyday lives. While his algorithm is still developing, the effects are far-reaching. His work could help find novel cures from antivirals to cancer treatments.
Monday, November 28, 2022
Dr. Peter Chung
Professor Chung’s research interests lie in biophysics and neurobiology, particularly looking at its applications in diseases such as Alzheimer’s and Parkinson’s. His most recent publication, “The C-Terminal Domain of ɑ-Synuclein Confers Steric Stabilization on Synaptic Vesicle-Like Surfaces”, focuses on the clustering structures of, ɑ-Synuclein, a protein linked to Parkinson’s.
Physics of a Table Fan, Abbey Bonino 11/28/22
Physics of a Table Fan
By Abbey Bonino
Over Thanksgiving break I was able to get together with my extended family, which included my wonderful, but naive, younger cousin. As we were all congregated in a small space, my mother had set out a couple table fans to circulate the air more effectively. Unfortunately, this prompted my cousin to almost stick his finger in the fan, claiming that because he “couldn’t see each of the blades anymore, they must not be there to hurt me.” I quickly explained to him that this was not true, and that putting your hand in the way of the blades could really hurt it!
As I thought about my explanation to get him to stop, it made me curious just how fast these fan blades were spinning – I could now apply my new knowledge of angular quantities to make sense of this situation! I found the box of the fan in our basement, which stated on the back that the revolutions per minute (rpm) of the blades on the “high” setting is 1,450 rpm. Converting this to revolutions per second (rps), this value is equivalent to 24.2 rps, or 24.2 Hz, which is the frequency (f). Taking the reciprocal of this value (1/24.2 rps) gives the period (T), being 0.0414 seconds per revolution. Then, as the angular velocity (ω) is equal to 2π/T, I calculated ω to be 151.8 radians per second. To make this value easier to conceptualize, I converted the angular velocity to linear velocity using the formula v = r ω. I measured the radius (r) of the fan to be 30.5 cm, which is 0.305 meters. This value allowed me to calculate the linear velocity, which comes out to be 46.3 m/s. This value is equivalent to 103.6 mph - the blades are spinning extremely fast, fast enough to harm you if you impede their movement with your hand!
Calculations:
Irish Dance Defying Gravity
This past weekend, I was watching my friends compete at the Irish Dance Regional Championship. I was a competitive Irish dancer my whole life, but I never realized the level of physics that is involved in this sport until our discussion of forces in our class! In Irish dance, one specific move requires you to push off the ground to do a leap in the air. This move is done in shoes similar to ballet shoes. A visual of the lead dancer of Riverdance performing this move is shown below.
You can see that due to the force of gravity on the dancer, they go up and come down relatively quickly. Newton's third law stating that "every force has an equal and opposite force" can also be seen between the dancer's foot on the ground and the ground pushing back on the dancer's foot to help propel her upwards into the air. It was obvious to me and my fellow dancers how much of a toll this sport takes on your bones and muscles, but we didn't quite focus on why certain injuries were so common. I had overuse tendon and muscle injuries multiple times a year, which I can now attribute to the level of force acting on my body when I would push off the ground to leap, like my friend here above :)
I wanted to take a look at what the actual value of a typical Irish dancer's force would be to push up off the ground. I used a mass of 40 kg with an average acceleration of 1.5 m/s^2. The calculations to find the force of a dancer's push off the ground are found below.
F | X | Y |
Fp | - | Fp |
Fg | - | -mg |
Inflatable Helmets
Inflatable Bike Helmets
When I was in Copenhagen, I noticed that most people wore bike helmets that inflate upon impact rather than standard bike helmets. Upon further research, I discovered that these helmets are advertised as much safer than standard helmets:
We know that standard helmets work by the helmet refill increasing the time over which the impulse acts. Simultaneously, the outer shell spreads the force to a larger area.
The inflatable helmet uses artificial intelligence algorithms to know when to inflate. The process in which the collar is converted into a helmet takes 0.1 seconds.
To determine which helmet is safer, I will compare the force upon impact when cyclists are going at the same speed, one wearing a regular helmet and one wearing the Hovding inflatable helmet.
The average speed of an amateur cyclist is 18mph or ~8.0 m/s.
So, if someone is biking at 8.0 m/s and gets into an accident, what is the force upon impact?
Let’s say the cyclists are both exactly 70 kg.
𝐹∆𝑡=∆𝑝⃑=𝐼𝑚𝑝𝑢𝑙𝑠𝑒
∆𝑝⃑=mv= (70kg)*(8.0m/s)= 560 Ns
Time for a standard helmet= 6 ms
Time for inflatable helmet= 36 ms based on Stanford data: “We found that airbag helmets, with the right initial pressure, can reduce head accelerations five to six times compared to a traditional bicycle helmet (Kubota, 2016).
The force upon impact for a standard helmet: ∆𝑝⃑/∆𝑡= F= (560Ns)/(6s)=93.33 N
The force upon impact for the inflatable helmet:∆𝑝⃑/∆𝑡= F= (560Ns)/(36s)= 15.56 N
Therefore, the force upon impact is ~6 times less with the inflatable helmet than with the standard.
How it works:
There are two aspects to the helmet’s function: the transformation from a collar to an airbag, and the functionality of the airbag itself. Researchers use an Artificial Intelligence algorithm for the helmet to detect when to inflate based on thousands of crash test videos. Inside the collar (helmet before inflation), a small gas inflator uses helium to inflate the airbag. The airbag stabilizes the neck and provides shock absorption. The pressure remains consistent so the airbag can sustain multiple head impacts during one accident, before it deflates.
Rotation:
We know that oblique impacts result in rotation of the head, to which the brain is most sensitive. Linear acceleration is mainly associated with the risk of skull fracture, but angular (rotational) acceleration and rotational velocity are associated with brain injuries. The airbag in the inflatable helmet creates a flexible area between the head and the ground that effectively absorbs the energy that causes harmful rotational force.
To test how different helmets perform when rotational force is involved, researchers compared the translational accelerations (g), rotational (angular) velocities (rad/s), rotational accelerations (krad/s^2), and strain (%) for different helmets on the market. Strain is the brain tension ratio caused by rotation of the brain (generated by computer simulation). A strain above 26% corresponds to a 50% risk for concussion. Diagrams and explanations of each of the four tests (shock absorption, oblique impacts 1,2, and 3) conducted are below:
Results of tests:
The Hövding 2.0 helmet performed almost three times better than all the other conventional helmets (48 g vs other helmets that were around 175 g for translational acceleration).
In the oblique impact 2 test (side of helmet), the inflatable helmet had the lowest rotational acceleration of 1.5 krad/s^2.
In the oblique impact 3 test (upper part of the helmet), the inflatable helmet had the lowest rotational acceleration of 1.7 krad/s^2.
For oblique test 4 (impact on the rear of the helmet), the inflatable helmet had the lowest rotational acceleration of 2.8 krad/s^2, with the average being 12.0 krad/s^2.
Overall, the inflatable helmet performed much better than other helmets in translational and rotational (linear and angular) collisions. This reduction in acceleration occurs because when the helmet is inflated, “the exterior fabric can slide sideways in relation to the fabric on the inside against the head, and two shearing layers are created that considerably reduces the rotational acceleration” (Olsson et al., 2017).
Sources:
https://hovding.com/2021/09/06/have-you-tested-a-hovding-we-have/
https://news.stanford.edu/2016/10/03/stanford-researchers-show-air-bag-bike-helmets-promise/
The Physics Behind Latte Art by Sarah Hiranandani
As I was sitting thinking about what I should write my physics news on, I was sipping a cup of coffee. This made me think about our current unit on fluids and buoyancy. I began to think about latte art and how is it that people can seemingly “draw” all kinds of pictures using steamed milk on top of a couple espresso shots already in the cup.
As we are beginning to discuss in class, the density of an object or in this case another liquid is crucial to our understanding of how it interacts with other liquids. I was perplexed by how if one were to just pour milk into a couple shots of espresso, without having frothed or steamed it first, it would simply mix with the espresso; however, if the milk is frothed or steamed first it begins to clump together in the latte and can create beautiful art as seen in the pictures above.
Milk is steamed most often in coffee shops using a steam wand that both spins the milk as well as heats it as it creates small bubbles in the milk to make more of a foamy texture. Because of this porous foam that develops, the milk begins to seemingly float on top of the espresso because it is able to “hold other liquids” in between its bubbles. Due to the foams elasticity, and ability to bounce back into shape, its able to hold these borders between the brown coffee mixture and the steamed milk.
This is in contrast to a layered latte when lighter/less dense espresso is poured into more dense milk. As we discussed in class, a denser object and/or fluid will fall to the bottom, which creates the layered affect seen in the picture below. This contrast is directly due to the difference in density of the two liquids, and the rate at which they are poured, as well as their temperature which results in them floating or being submerged. The density of milk at 38.9 degrees celsius is 1.026 kg/L3 while the density of espresso is only 1 kg/L, and therefore is less than most milk's when steamed. So, we can use this density to our advantage and create some fun latte art or a nice layered latte.
Sources
Defining Espresso (2020), Parchmen & Co., Article: https://www.parchmen.co/blogs/writing-about-our-passion/defining-espresso#:~:text=As%20such%2C%20given%20that%20the,or%20%3E%201%20gm%2Fml
The Physics Factbook: An Encyclopedia of Scientific Essays:
https://hypertextbook.com/facts/2002/AliciaNoelleJones.shtml
Uyeno, Greg, “How does latte art work?” Live Science https://www.livescience.com/55696-how-does-latte-art-work.html
Images:
https://www.lesswastecoffee.com/barista-pen-for-latte-art.html
https://eldoradocoffee.com/blogs/news/latte-art-home
Pavel Kroupa by Zach Martin - Nov 12
Sunday, November 27, 2022
Tad Pfeffer and the physics of skiing
Tad Pfeffer is a glaciologist, geophysicist, and photographer. He earned his bachelor's degree from in geology, his master's in geology, and his Ph.D. in geophysics. His research is focused on glacier mechanics and dynamics. Currently, he is doing research at the University of Colorado in Sea level rise, hydrology, natural hazards, geophysical and architectural photogrammetry, and science policy. The article that caught my interest is from 2009 when he did research with two other physicists on the physics behind ski moguls. Essentially what they found is that throughout a ski season, moguls move about 10 m uphill. This is surprising because the typical motion of skiers is downhill. This is essentially done by skiers scrapping off the downhill side of the mogul and pushing it down to form a new mogul. Another interesting finding they had was that despite the complete randomness of skier's patterns on the slope, the moguls always form in almost completely uniform ways.
The physics of a chuck it (dog fetch toy)
Over thanksgiving break, I was playing fetch with my dog. My dog is pretty fast so we use a chuck-it ball launcher to throw the ball extra far. While throwing the ball for him, I noticed that there had to be some physics involved with the item. For reference, a chuck-it looks like this when it is being thrown:
So why does a chuck-it increase the distance a ball can be thrown? The chuck-it is designed to be an extension of someone's arm. Thinking about torque, the chuck-it increases the radius of someone's arm. The equation for torque is Torque = Force * Radius. Assuming a person does not get a massive strength increase by using the chuck-it, we can assume the force they exert using the chuck-it is the same as the force they would exert on the ball alone. Thus, with the same force and a greater radius, the torque is much greater using the chuck-it. This increase in torque means that a greater force is acting on the ball. If a greater force is acting on the ball, the displacement is larger because displacement is proportional to force. Additionally, this explains why people with longer arms are able to throw the ball farther than people with short arms.
Slippery Roads
On my drive back to Hamilton, NY after Thanksgiving, it was pouring rain almost the entire way. My parents had warned me to drive slowly and be very cautious, this is because the rain on the road causes the road to become very slippery, the physics of friction can explain this. The slipperiness is caused by a lack of friction between the road and the tires. This is because as the tires move over the road with water on them, the water is filling in the tiny pores on the road and smoothing out the surface. This then makes the friction that is usually present on a dry road disappear and slipperiness is formed.
There were at least two instances on my drive where I felt my tires skid and cause the wheel to shake, I was able to gain control of the car, but it was very scary to actually feel the car lose control due to the heavy amount of water that was on the road. When driving in the rain, it is super important to keep in mind the physics of a wet surface.
Dr. John Eric Geoff and the Physics of Sports
Dr. John Eric Geoff is a sports physicist, who currently conducts sports physics research at the University of Lynchburg located in Lynchburg, Virginia. Dr. Geoff graduated from Vanderbilt University in 1992 with a Bachelor’s Degree in Physics and Mathematics and later got a Ph.D. in Physics with his thesis on “Theory of Photon Drag Effect in Simple Metals” which he completed at the University of Indiana. Since acquiring his Ph.D., Dr. Geoff has published numerous journal articles with topics ranging from the Tour De France to the current World Cup in Qatar.

Dr. Geoff currently researches computational electrodynamics, which is essentially modeling an electromagnetic field within an environment as it relates to that object in the environment. In past years, he has written articles on head collisions and acceleration of male lacrosse players, which is similar to the football problem we discussed in class. Interestingly, he has also worked to create prediction models for college football teams as well as the Tour De France for racing and competing. Aside from his current research, Dr. Geoff has also written a book titled Gold Medal Physics: The Science of Sports, which is meant to be an introduction to the physics of Olympic sports, while remaining at the level of introductory physics. He discusses a number of physical phenomena in sports and well-known athletic accomplishments such as David Beckham’s bent soccer kicks, Lance Armstrong’s Tour De France, Olympic diving, and many other sports. Most recently, he has published on the seam geometry, and shape of soccer balls and what effect this has on the aerodynamics of a soccer ball.

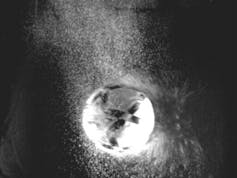
I found Dr. Geoff through an article entitled “World Cup: This year’s Al Rihla ball has the aerodynamics of a champion, according to a sport’s physicist.” As Dr. Geoff notes in the article, one of the most important aspects of the soccer ball is how it travels in the air as many amazing plays actually happen while it is in the air. He discusses the importance of the boundary layer which is essentially the layer of air that is just around the outside of the ball, which expands when the ball is traveling at higher speeds and is only concentrated around the front of the ball at the lower speeds. Interestingly, Dr. Geoff notes that a rougher ball has less drag resistance, which may seem counterintuitive. To account for this, the current ball called the Al Rihla ball has wider and deeper seems than previously and therefore is able to travel through the air more easily with less drag. As someone who watches a lot of soccer and is particularly excited about the world cup, it was interesting to read about how the soccer ball this year is different from previous World Cups. This article has much more to offer besides just the work of Dr. Geoff, so I have attached it below!
Professor Erwin Neher and the fascinating field of biophysical chemistry
Erwin Neher, (born March 20, 1944, Landsberg, Germany), is a German biophysicist who was a co-recipient, with Bert Sakmann, of the 1991 Nobel Prize for Physiology or Medicine for "their discoveries concerning the function of single-ion channels in cells." This was possible due to their invention of the "patch-clamp" technique, a laboratory method that can detect the very small electrical currents produced by the passage of ions through the cell membrane.
Dr. Neher earned an undergraduate degree in physics from the Technical University of Munich and then attended the University of Wisconsin at Madison (through a Fulbright Scholarship), where he obtained a master of science degree in 1967. From 1968 to 1972, Neher did his graduate and postdoctoral work at the Max Planck Institute for Psychiatry, Munich. He first developed the idea of the patch-clamp technique in his doctoral thesis and earned a Ph.D. from the Technical University of Munich in 1970. In 1972 Neher attended the Max Planck Institute for Biophysical Chemistry, Göttingen, and began his collaboration with Sakmann two years later. In 1976, Neher returned to the Max Planck Institute for Biophysical Chemistry, where he held the position of Director of the Membrane Biophysics department from 1983-2011.
Patch clamp biophysics - The membrane of a cell contains numerous pore-like channels that control the passage of ions, or charged atoms, into and out of the cell. Neher and Sakmann used an extremely thin glass pipette, one-thousandth of a millimetre in diameter, that was fitted with an electrode to detect the flow of individual ions through the ion channels of a cell membrane. The technique was used to study a broad range of cell functions. During a "patch clamp" recording, a hollow glass tube called a micropipette or patch pipette which contains an electrolyte solution and is connected to a recording electrode is brought in contact with an isolated cell of interest's membrane, thus forming an electrical circuit. This technique made it possible, for the first time, to record the currents of single ion channel molecules which improved our understanding of the roles that these channels play in fundamental cell processes such as action potential and nerve activity of CNS-associated cells.
Apart from the 1991 Nobel Prize in Physiology or Medicine, Dr. Neher has several accolades, most of which he has shared with Dr. Sakmann -
| Nernst-Haber-Bodenstein, Award of the German Society for Physical Chemistry 1977 | |
| Feldberg Award, Feldberg Foundation, London 1979 | |
| K.C. Cole Award, Biophysical Society 1982 | |
| Harold Lamport Award, New York Academy of Sciences 1982 | |
| Spencer Award, Columbia University 1983 | |
| Adolf Fick-Preis, Universität Würzburg 1984 | |
| Louisa Gross-Horwitz Award, Columbia University 1986 | |
| Fidia Research Award Lecture, Fidia Research Foundation 1986 | |
| Schunck-Preis, Universität Giessen 1986 | |
| Leibniz Award, Deutsche Forschungsgemeinschaft 1986 | |
| Gairdner Award,Toronto l989 | |
| Hans Hellmut Vits-Preis, Universität Münster 1990 | |
| Bristol-Myers Squibb Research Award, New York 1990 | |
| Gerard Prize, American Neuroscience Association 1991 |
Sources:
Encyclopædia Britannica, inc. (n.d.). Erwin Neher. Encyclopædia Britannica. Retrieved November 27, 2022, from https://www.britannica.com/biography/Erwin-Neher
The nobel prize in physiology or medicine 1991. NobelPrize.org. (n.d.). Retrieved November 27, 2022, from https://www.nobelprize.org/prizes/medicine/1991/neher/biographical/
Sakmann, B., & Neher, E. (1984). Patch clamp techniques for studying ionic channels in excitable membranes. Annual Review of Physiology, 46(1), 455–472. https://doi.org/10.1146/annurev.ph.46.030184.002323
Veitinger, S. (2022, November 18). The patch-clamp technique. Science Lab | Leica Microsystems. Retrieved November 27, 2022, from https://www.leica-microsystems.com/science-lab/the-patch-clamp-technique/?tx_leicacontacts_pi1%5Bcontroller%5D=Contacts&tx_leicacontacts_pi1%5Bcountry%5D=MZ&cHash=51407dd3ff5ecdc974e87088c66bf1b9
The Physics of Horseback Riding
Over Thanksgiving break, I competed in a horse show at Skidmore College. As I was watching the jumping classes, waiting for mine to begin, I was thinking about how horses are able to jump over things. It quickly occurred to me that physics is involved. Kinematics, forces, and energy are all key components of the horse being able to jump.
The motion of a horse going over a jump reminded me of the projectile motion problems we looked at in class, specifically, the springbok jumping problem. The horse leaves from the ground, which could be considered y = 0m, and reaches the highest point of the jump before returning to the ground. There is motion in both the x and y directions. This motion could be analyzed using kinematics.
Lastly, energy can be used to analyze the motion of a horse jumping because energy is connected to motion and the ability to cause motion. As the horse moves towards the jump, it has kinetic energy defined as KE = ½mv2. As the horse jumps, most of that energy becomes potential energy, defined as PE = mgh, because the horse itself is not actually moving, it is simply flying through the air. Once the horse lands again, the energy transforms back into kinetic energy. Although I am not positive what the forces would be, I am sure that there are also non-conservative forces acting on the system, perhaps air resistance, friction, or even the force of the push off the ground. The equation that could be used to analyze this is △KE = -△PE + Wnc.
There are just some of the ways that I could think of in which horseback riding is related to physics, but I am sure there are many other ways in which the two are related!