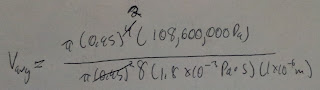Thermodynamics, Refrigerator, and Air Conditioner

By Xinke Liu

Many people may have wondered if we could make a room cold by leaving a refrigerator door open? In fact, I tried it when I was a kid. But I never had the patience to see what happened. After learning the second law of thermodynamics, I thought this explains why a refrigerator cannot cool a room.

The second law of thermodynamics states:

Heat can flow spontaneously from a hot object to a cold object; heat will not flow spontaneously from a cold object to a hot object.     

If a refrigerator cannot cool a room, how does air conditioner work? Does air conditioner work against the second law of thermodynamics?   

The second law of thermodynamics only offers partial explanation to the problem.

The Clausius statement of the second law of thermodynamics gives us a better idea, which states:

No process is possible whose sole result is the transfer of heat from a body of lower temperature to a body of higher temperature.

Both refrigerator and air conditioner are essentially ‘heat pumps!’ Work must be done to make heat flow from a body of lower temperature to a body of higher temperature.

Refrigerator and air conditioner are composed of evaporator, condenser, and compressor.

Evaporator transfers heat from hot air to fluid. Condenser transfers heat from fluid to outside air. Compressor does work on the fluid by compressing it and creating entropy.

If we leave a refrigerator door open, the room would warm up because the condenser is also inside the room. The condenser dumps heat out into the room all the while that it's running. And because the fridge is not 100% efficient, there will be more heat generated than there will be cooling.

How much heat can an air conditioner remove from a building’s air per second?

Let’s assume coefficient of performance is 2.0 and the air conditioner is rated to do work at 1000W.

QH= COP * W = 2.0 * 1000W = 2000 J.

An air conditioner with coefficient of performance is 2.0 and the air conditioner is rated to do work at 1000W can remove heat from a building’s air at a rate of 2000J, or at a rate of 2000W per second.

Scuba Diving Physics: Why people suffering from hearing loss cannot dive?

Written by Xinke Liu

Ever since Jacques-Yves Cousteau made the Great Blue Hole of Belize famous in 1971, this amazing wonder has lured thousands of scuba diving fans to explore it. The Great Blue Hole is said to be the largest blue hole in the world and has a perfect circular shape. This site is a great place to have a prehistoric journey to see remnants preserved from millions of years ago. You will have fascinating experience of swimming with SHARKS and freaky fish in the crystal clear water!!!! Myths say that the charming blue in the Great Blue Hole entices some divers to stay there FOREVER…. FOREVER…FOREVER…

Sadly, people suffering from ear diseases and hearing loss like me cannot dive. What’s keeping us away from this fascinating activity? One reason is that some of them may also have problem in balance that is controlled by the vestibular system in inner ear. But the major reason is, not surprisingly, pressure.

The Great Blue Hole is 412 feet deep. Most divers dive down to between 110 and 130 feet. How much pressure does the water exert on the eardrum when people are 130 feet deep into the sea?

The pressure P due to the weight of liquid is:

P = pgh.

We need to find out the density (p) for the water in the Great Blue Hole since density of seawater varies due to temperature, pressure, and salinity. Since the salinity of the seawater in the Great Blue hole is not as unusal as that of the seawater in Dead Sea, we would take the average value of density of surface surface seawater that is 1.025 *10³  kg·m³.

130 feet ≈ 39.6m.

g = 9.8 m/s².

P = (1.025 *10³  kg·m³) * (9.8 m/s²⁾ *(39.6m) ≈ 397782 N/m².

P ≈ 3.98*10⁵ Pa.

1 atm = 1.013 ×10⁵ Pa.

P/ 1 atm = (3.98*10⁵ Pa) / 1.013 ×10⁵ Pa ≈ 3.9 atm .

When people are 130 feet down in the Great Deep Hole, the water exerts 3.9 atm of pressure on the eardrum, almost 4 times of the average atm level on sea level. And this could be a disaster to people with hearing problem. And when diving, eardrum is in direct contact with the water.     

Some people may wonder why not divers just use earplugs to protect eardrum. However, in fact, earplugs are not recommended when diving. The graph below shows that fluids exert pressure on object from every direction. This means the seawater would push the earplug inside the ear.     

Physics of Flight

Physics of Flight

            For my physics news I decided to look at the physics of flight. There are four main forces involved in flight. They consist of an upward force, lift, a downward force, weight, a forward force, thrust, and a backward force, drag. In order for flight to occur, lift must be greater than or equal to the weight and thrust must be equal to or greater than drag.

            The wings of a plane are responsible for providing the lift. This concept can be explained by both Bernoulli’s principle and by Newton’s third law. As air currents pass by the wings of a plane, their shape, airfoil, establishes a differential pressure gradient. The distance the air has to travel is greater above the wing than below the wing. Since the air travels past the wing in the same amount of time, the air above the wing moves faster than the air below the wing. Bernoulli’s equation (P1 + .5pv1^2= P2 + .5pv2^2) indicates that this increase in speed causes a decrease in pressure above the wing and an increase in pressure below the wing. This unequal pressure causes dynamic lift, which pushes the plane upwards. The angle of the wing also plays a role in providing lift. The wing directs wind downwards as the plane flies. As established by Newton’s third law, the downward wind molecules push the wing in the opposite direction that they are traveling.

            The thrust of the plane comes from the engine or propeller. Like lift, it also utilizes Newton’s third law. Air is sucked in to the engine and pushed backward. As the air moves back at a rapid rate, the plane gets pushed forward. With the aide of an engine, the air traveling back causes a greater force than the wind on the body of the plane.

            Both Drag and weight limit the ability of the plane to fly. As wind hits the plane, it pushes the plane in the opposite direction that it wants to travel. In order to limit drag, planes have been designed to lower the surface area of the body. By doing this, the path of the air is less hindered, therefore causing less drag. The weight force is simply the force of gravity and the mass of the plane.

            Now that I have explained the physics behind flight I will look specifically at the Boeing 747 jet airplane to mathematically show these principles.

Force Weight= mg

Force Thrust= ma

Force Lift= C* (.5pv^2) *wing A

Force Drag= C* (.5pv^2)*Total A

FW=(333,390kg)(9.8m/s^2)=3267222N

FT=(333,390kg)(a) FT= 4(223000N)

(4*223,000N)/333,390kg = 2.7m/s^2

Acceleration seemed slow to me but this is due to the fact that it is a commercial plane. They accelerate very slowly over a long period of time.

FW=FL 3267222N= C* (.5*1.29*(265.3m/s)^2*510.95m^2 C=.14 constant

FD=FT 892000N= .022* (.5*1.29*(265.3m/s)^2 *A   A=893m^2

How much tension is there on a guitar string?

By David Haimes

The lowest note possible on a guitar is the open low E string. Using a guitar-tuning app
on my phone, I measured the frequencies to be about 80 Hz.

Given
Frequency: 80 Hz
Length: About 25 inches from fixed point to fixed point
Mass: 10 grams (very rough estimate/guess)

The Force due to tension equation is

FT = ( m / L ) * v2

We need to find v.

The equation for v is: v = ƒλ
And λ = 2L = 2 (25 inches * (.0254 m / 1 inch) ) = 1.27 m

Now we can solve for v : v = ƒλ = 80 Hz (1.27 m) = 101.6 m/s

Now we can solve for FT= ( .010 kg / (25 inch (.0254m/1 inch) ) * (101.6 m/s)2 = 65 N

So the approximate tension on the string is 65 N

The website lists the recommended tension for the string on my guitar to be 27 lbs which
is about 120 N. Assuming all the calculations are correct, the one big assumption/
approximation I made was the mass of the string. Working backwards, a tension of 120 N
would require a mass of…

m = FT / (v2*L) = 120 N / (101.6 m/s * 1.27m) = .0092 kg

I plan to bring the string to lab on Thursday to see how close the mass of the string is to
this! However, the string is larger than length used in the equation, due to excess beyond
the fixed points.

Paintball Physics

By Michelle Lu

Kids often bruise when they are hit by a paintball if they’re not wearing a vest.
Let’s see how much force a paintball would be exerting on you if you were hit by a
paintball.

I chose to assume there is no air resistance. Target is at a distance of 50 ft and you
are shooting at an angle of 15° at 300 ft/s. The ball stops in 0.001s once it hits the
target.

m = 3.2 g = 0.0032 kg
vo = 300 ft/s = 91.4 m/s
v0x = 91.4cos15 = 88.3 m/s
voy = 91.4 sin15 = 23.67 m/s
Θ = 15°
Δx = 50 ft = 15.24 m

Δx = voxt + 1/2at2
15.24 = 88.3 t + 0
t = 0.17 s

Δy = vot + 1/2at2
Δy = (23.67 m/s)(0.17s) + ½(-9.8 m/s2) (0.17s)2
Δy = 3.88 m

vfy2 = voy2 + 2aΔy
vfy2 = (23.67 m/s)2 + 2(-9.8 m/s2)(3.88 m)
vfy = 22.0 m/s

vf = (vfx2 + vfy2)1/2
vf = (88.32 + 22.02)1/2
vf = 91 m/s

F = Δp/t
F =m(vf – vi)/t
F = [(0.0032 kg)(0 m/s – 91 m/s)]/0.001t
F = 291 N

Analyzing traffic patterns using fluid motion

By Lauren Charette

By using the average speed of cars on a highway and the number of lanes as the radius we can
get an idea about the ration of the number of cars on the road in a given area and understand the
amount of traffic.

Given the equation:

Q=AV

If the cars are moving at a speed of 27 m/s And the road is four lanes wide a lane being 3ms so
we’ll give it an r value of 12m and we’ll look at a 10m length so for this part the area is 120m2

Q=27*120

Q=3240
If the velocity is consistent but the number of lanes is reduced to 3 what happens to the speed?

Q=90*27

Q=2430

However because bottlenecking causes cars to slow down if the speed is reduced five m/s what is
the rate of flow?

90*22=Q

Q=1980

Physics of fighter jets

By Paul Donohue

I’ve always been interested in fighter jets, particularly of how they are able to take off and land on an aircraft carrier. They are able to accelerate so rapidly with the aid of a steam powered catapult. See below:

The release of a great deal of pressure in the form of steam drives the piston of the catapult forward, bringing the plane with it. In finding just how large the magnitude of work done by the catapult might be, I had to do some research. I found that the standard length of a catapult track is 72.8 m and the thrust of a F-18 super hornet’s engines is around 3.9x105 N collectively. I estimated that the fighter would have 6.03x107 J of Kinetic Energy at takeoff meaning the work done by the catapult is:
=6.03 x 107 - 3.90 x105*72.8=3.2*107J.

Physics of Ski Jumping

By Paul Donohue

Ski jumping performance is a result of not only the aerodynamic equipment used but also the motor skills and size of the jumper. Anorexia Nervosa and Bulimia were common disorders among elite jumpers up until recent regulations. The forces involved from takeoff to landing are numerous including gravity, air resistance, torque, centrifugal, and even lift which will be the focus of my investigation. I’d like to estimate just how much lift force is generated by those large skis.

On the ramp the jumper must try to minimize the frictional force between his/her legs and the snow (i.e. being light) and also the aerodynamic drag force to reach a maximum v0 Because the ramp is curved at its end the jumper experiences a good deal of centrifugal force for which he/or she must counteract to obtain a maximum momentum perpendicular to the ramp’s takeoff. At takeoff, the jumper must try to anticipate the torque force exerted by the air stream that threatens to tip him/her backwards into a bad flight position. This is done by directing angular momentum forwards….though not too far or tumbling can occur! Once in flight gravity, lift, and drag affect the jumper

Lift can be solved for the equation FL=(1/2)LcL ρv2 where L refers to surface area and cL is the lift coefficient with a value of .4 (typical values range from .4 - 1)
• First we’ll set v to 25 m/s: This is the sum of v0 and vp which is the
velocity perpendicular to the ramp.
• The surface area of one ski is .32 m2 and the density of air is 1.225 kg/m3
(1/2)(.32*2)(.4)(252)=80 N of Lift!

The reason ski jumping isn’t as dangerous as it may look is that the landings are engineered to only be roughly 3o below the axis of the skier’s trajectory If the launch angle is -9.5o above the horizontal (ski jumps actually don’t slope upwards) and the launch velocity is 25 m/s then…25sin(-9.5)= -4.13 m/s in the y-direction and 25cos(-9.5)=24.66 m/s in the x-direction If the skier travels 55.0 m horizontally to the landing zone then 55.0/24.66=2.23 s

During this time, gravity will increase the rate of to descent to 4.13+(-9.8)(2.23)= -17.7 m/s
Tan-1(-17.72/24.66)= -35.7: The angle of the skier’s trajectory is 35.7o below the horizontal which minus 3o would mean 32.7o below the horizontal for the landing slope!

Single Pendulum and the Earth

By Manjie Huang

Can a lighter object be accelerated sufficiently to lift a heavier object?

By Ali Pesch

The focus of my second physics news is centered on the question, “can a lighter object be accelerated sufficiently to lift a heavier object?” To attempt to answer this question, I viewed a YouTube video (link below) that depicted the question I am asking. In the video, a string is pulled through a drinking straw and then attached to a small AA battery to one end and 3 batteries to the other end. Holding the straw firmly, the single battery is hurled into rotation, orbiting around the axis of the straw. With increasing speed, the orbital radius increases. At some point, the centrifugal forces exceed the gravitational pull of the 3 AA batteries, and they lift off.

The experiment described above uses the formula a = υ 2 r -1 with “a” signifying acceleration, “υ” representing constant speed, and “r”  being the radius of the circle. In addition, we need to use the equation F = ma, as it follows that the force is the acceleration multiplied by the mass of the battery. The forces in play include the centrifugal pull exerted by the orbiting single battery, that is opposed by the force of tension of the string connected to the weight of the 3 AA batteries attached to the other end. As Newton’s Third Law of Motion suggests, the increasing rotational speed augments the centrifugal vector. At some point, it exceeds the centripetal vector exercised by the 3 AA batteries and these lift off. The force needed to lift off the 3 AA batteries follows Newton's Second Law of Motion F = ma, where “F” stands for force, “m” symbolizes mass and “a” signifies acceleration. In other words, acceleration is produced when a force acts on a mass; heavier objects require more force to move the same distance than lighter objects. The motion in this experiment is not linear but is circular. We are only interested in the force that is necessary to lift the 3 AA batteries up higher into the air. The orbiting battery is being accelerated along a circular path with steady speed while constantly changing its direction tangentially to the orbital circle. Here, the centripetal acceleration is a radial acceleration and can be calculated as ac = υ2 r -1 where “υ” is the constant speed of the object along the circular path and “r” equals the radius of the path. In the experiment, the average weight of a single AA battery is 23 grams (0.023 kg). Below are my calculations:

m1 = 0.023 kg

m2 = 0.069 kg

m2 = 3m1

r = 0.20 m.

Solution

(0.023 kg)(ac) = (0.069 kg)(9.8m/s2)

ac = 29.4 m/s2

ac = υ2 r -1

(.2)(29.4) = υ2

υ = 2.42 m/s


If we want to take it a step further we can find θ.

Solution

Fc = mac

Fg2 = 3Fg1 = Fc

m1ac = m2g

tan(θ) = 3x/1x = 3

tan-1(3) = θ

θ = 71.6o

Alternative

a/g = m2/m1

υ2/ (g)(r) = m2/m1

In this case, the 3 batteries have 3 times the mass of 1 battery, so ac must equal 3g. Overall, a smaller object can accelerate sufficiently to lift a heavier object if the magnitude of the centrifugal acceleration exceeds ag by a factor equal to the factor that the magnitude of the larger mass exceeds the smaller mass by.

This principle is used in commercial applications, such as the centrifugal clutch in vehicle transmissions.

Fg1 = Fg2

θ = tan-1(m2/m1)

http://www.youtube.com/watch?feature=player_embedded&v=DbUU-ueiPUc

Physics of a Spinning Ballerina

By Farah Fouladi

The forces acting on a dancer
- Gravity (downwards)
- Normal Force from the floor (upwards)
- Friction of the floor

Turns in ballet (the physics terms we can use to describe it)
- Angular velocity = how fast the dancer is spinning
- Rotational Moment of Inertia

A fouette is based of the principal of a moment of inertia.
- When the dancer starts turning her arms are brought together
o Small radius
r = 0.2 m
o Small moment of inertia
Treat the dancer’s body as a solid cylinder
Mass of dancer = 55 kg
I = ½ mr2 = ½ (55 kg)(0.2)2 = 1.1 kg m2
o Thus a large angular velocity
Let’s say 1 rad/s
o L = Iw
= (1.1 kg m2)( 1 rad/s) = 1.1 N m s
- The dancer stops for a second and extends her arms and legs
o Larger radius
r = 0.4 m
o Larger moment of inertia
Treat the dancer’s body as a solid cylinder
Mass of dancer = 55 kg
I = ½ mr2 = ½ (55 kg)(0.4)2 = 4.4 kg m2
o Smaller angular velocity
w = L/I
= (1.1 N m s) / (4.4 kg m2)
= 0.25 rad/s
- The dancer continues turning with arms brought together
o Small radius
o Small moment of inertia
o Thus a large angular velocity

How does the dancer stay balanced?
- This is based on canter of gravity!
- Before spin:
o Top half of body is symmetrical
o Vertical center of mass is at center of middle axis
o Legs are not, one leg is straight and the other is in passé

o Xcm = ((xtop)(mtop) + (xrightleg)(mrightleg) + (xleftlef)(mleftleg))/(mtot)
o Xcm = ((0)(29) + (0.2 m)(13 kg) + (- 0.05 m)(13 kg))/(55 kg)
o = 0.04 m shifted to the right!
- After spin:
o Top half of body is symmetrical
o Vertical center of mass is at center of middle axis
o Legs are not, one leg is straight and the other is in fully extended
o Xcm = ((xtop)(mtop) + (xrightleg)(mrightleg) + (xleftlef)(mleftleg))/(mtot)
o Xcm = ((0)(29) + (0.6 m)(13 kg) + (- 0.05 m)(13 kg))/(55 kg)
o = 0.13 m shifted to the right!
So a dancer must constantly adjust to its new center of mass while turning at all
times!!

The effect on a dancer’s body:
- To rotate faster, a dancer must DECREASE her moment of inertia.
- Can do this in 2 ways:
o Decrease mass
o Make sure the bulk of the body is close to the axis of rotation
o See how this correlates to ballerinas needing to very very thin!

Determining the Most Powerful Pokémon

By J.T. Ahearn

Blastoise:
Height: 5’3”
Weight: 189 lbs

Pokédex: Blastoise can pump out as much water as an Olympic size swimming pool
every minute.

Blastoise emits water from to cannons mounted on its back.

Olympic pool dimensions: 50mx25mx2.0m
Volume=2500m3

Q=vaveA
Cannon diameter: 0.1m
A=π0.05m2x2=0.0157m2
Q-2500m3/60sec=41.7m3/sec
41.7m3/sec=vave(0.0157m2)
vave=2700m/sec

Hydro pump fires approximately 1 liter (0.001m3) of water at the opponent.
m=ρ/V
m=1000kg/m3/0.001m3
m=1kg

v=680m/sec
m=39.5kg

KE=.5mv2
KE=.5(1kg)(2700m/sec)2
KE=3.65x106J

p=mv
p=(1kg)(2700m/sec)
p=2.70x103W

 

Pidgeot:
Height: 4’11”
Weight: 87 lbs

Pokédex: Pidgeot can fly two times faster than the speed of sound

v=680m/sec
m=39.5kg

KE=.5mv2
KE=.5(39.5kg)(680m/sec)2
KE=9.16x106J

p=mv
p=(39.5kg)(680m/sec)
p=2.69x104W

 

Machamp:
Height: 5’3”
Weight: 287 lbs

Pokédex: Machamp can punch Pokémon to the moon.

ve=escape velocity (velocity necessary to break a planet’s gravitational pull)

ve2=2GM/r

G=universal gravitational constant=6.67×10−11 m3/kg s
M=mass of planet
Mearth=5.98x1024kg
r=radius of planet
rearth=6.38x103km

ve2=(2)(6.67×10−11 m3/kg s)(5.98x1024kg)/(6.38x103km)
ve=350,000m/sec

mhuman fist=0.7kg
mhuman=70.0kg
A fists’s mass is approximately 1 percent of organism’s mass
mmachamp=130kg
mmachamp fist=1.30kg

v=350,000m/sec
m=1.30kg

KE=.5mv2
KE=.5(1.30kg)( 350,000m/sec)2
KE=7.96x1010J

p=mv
p=(1.30kg)( 350,000m/sec)
p=4.55x105W

 

Dragonite:
Height: 7’3”
Weight: 463 lbs

Pokédex: Dragonite can circle globe in 16 hours

rearth=6.38x103km
C=2πr
Cearth=2π(6.38x103km)
Cearth=4.00x107km

∆x=vt
4.00x107km=v(57,600 sec)
v=2400m/sec
mdragonite=210kg

KE=.5mv2
KE=(.5)(210kg)(2400m/sec)2
KE=6.05x108J

p=mv
p=(210kg)(2400m/sec)
p=5.00x105W

 

Diglett:
Height: 0’8”
Weight: 2 lbs

Pokédex: Diglet can pull itself underground at the speed of light.

v=3.0x108m/sec
m=0.91kg

KE=.5mv2
KE=.5(0.91kg)(3.0x108m/sec)2
KE=4.12x1016J

p=mv
p=(0.91kg)(3.0x108m/sec)
p=2.73x108W

The physics of funneling

By Kathryn Taylor

Being college students we have all seen people funneling beers at parties and we all
have that one friend who seems to be able to do it so much faster than everyone else!
The art of funneling is all in the physics.


Funneling all relates to Bernoulli's principle and the movement of fluids.

Using the Bernoulli's equation:

1/2pv^2 + pgh + P = constant

And the stated assumed values I was able to find that the final speed of the liquid was around 4.89m/s. Using this value in the equation of continuity: dV/dt = Av I found that the time taken for a 12oz (0.000355m^3) beer to pass through the funnel would be 0.14s.

We can also use the reynold's number to find out if the flow of the beer would be
turbulent or laminar. I found an RN of 69693 meaning that the flow is definitely turbulent, which is what makes this so difficult to do quickly!

Along with the turbulence there is also a large decrease in the radius of the hose and the persons throat, increasing the velocity, so making it much harder.

Base Jumpin’

By Allie Dyer

Base jumping is an activity where a person jumps off a high structure of
some kind with only a parachute to break their fall. In this video, this Russian base
jumper had some difficulty opening his parachute during this 120 meter fall. http://
www.youtube.com/watch?v=sJ59bNDhJcA
I wanted to know with what force he hit the initial snow and also how far
through the snow he travelled before stopping.

I assumed that it only took about .3 seconds to come to a complete stop from hitting
the initial snow.

V, or velocity, in this problem refers to the terminal velocity of the jumper.
According to the Physics Hypertextbook (http://physics.info/drag/) the typical
skydiver has a terminal velocity of about 55 m/s. This is the velocity needed to
find the force of the impact. But just to make sure I used the Drag Force formula of
Vt=√(2mg/CρA). because I wasn’t sure if this was the same for base jumpers.
For cross sectional area I assumed he was falling on his back/stomach because this
is where most of his injuries occurred so I decided to use a rectangular shape to
determine the cross sectional area of .51 m^2.

Vt=√(2mg/CρA).
Vt=√((2*83.8kg*9.8m/s/s)/(1.0*1.29kg/m^3*.51))
Vt=50. m/s

Using this formula I found a terminal velocity closer to 50m/s. I then could affirm
this velocity by using energy principles (∆KE=-∆PE) to solve for final velocity before
impact.
Vf=√(2gh)
Vf =√(2*9.8 m/s^2*120 m)
Vf=50. m/s.

To find the force with which the man hits the ground, use the equation F= ∆P/∆t
F=0-(83.8kg)(50m/s)/.3s
F=1.4*10^4 N

The Human Slingshot

By Adam Wheeler

The situation I decided to do my physics news on is the Human Sling Shot.
A person is harnessed into the middle of two bungees and secured so that she does
not actually leave the harness when it is pulled back. Then an ATV hooks up to her
via the back of the harness and then takes off in the opposite direction until the
bungees are stretched significantly. Then it is released and the woman begins to fly
forward with a great amount of speed and recoils backwards until coming to a stop.
I decided to try and determine the distance that she would have gone if she was not
connected to the bungee and could actually fire out of the harness.

http://www.youtube.com/watch?v=u2-od4n5Xl0

KNOWNS:

Mass of the woman: 60 kg
K spring constant: 53 N M
Height of the poles connected to the bungee: 30 meters
θ of the bungee with regards to the pole: 20°
woman is 1.5 meters from the ground
she is shot an an angle of 45° with respects to the horizontal
the bungee length is 31m
we assume the bungee is massless

First, I found the length of the bungee cord when she was just hanging there and not
being stretched back.

Cos(20°)= 29m/X

X=29m/Cos(20°)
X=31m

Next I found the PE of the system of the girl plus the two bungees:

PE= 2(1/2* 53N*M * (30m)2) = 48,000 Joules

Therefore,

PE1 = KE2
48,000= .5(60)v2
40m/s= v

Next, we can take this velocity and say that

KE1 = KE2 + ΔPE

48,000= (60)9.8m/s2(-1.5) + .5(60)(vf)2
49,000=.5(60)(vf)2
40.4 = v

Then we find the time it takes the person to land in the y direction

Δy= V0t +.5at2

-1.5= 28t + -4.9t2

-4.9t2 + 28t +1.5=0

Quadratic formula gives: 5.8 seconds

Therefore we can find ΔX from ΔX= X0 + v0t +.5at2

ΔX= V0t
ΔX= Cos(45°)40(5.8)
ΔX=160m

The force the ground exerts on her when she hits the ground is:

F=Δp/Δt. If it takes her .5 seconds to stop then the force is equal to:
F=60(-40.4)/.5
F= -5000Newtons.

Physics of Parkour

 By David Haimes

Parkour is the French art of movement, in which a traceur (someone who does parkour) moves in the most efficient way possible to get from point A to point B. Using our environment as an obstacle course, we use a variety of rolls, climbs, vaults and sometimes flips to traverse varying terrains. Since efficiency is so engrained in the very nature of parkour, the next logical step is clearly to study the physics of parkour to find ways traceurs can more efficiently perform movements and traverse an environment. I will analyze various movements and the related physics to see what patterns emerge and can make me a better traceur.

The roll and the flip – (roll demonstration: http://www.youtube.com/watch?v=5tJAyNxig_A)

A parkour roll is typically used to help lengthen the duration of an impact from jumping from a height. Both the parkour roll and the flip have very similar physics, as they are both rotational movements.

From our circular motion equations, we know the force of rotation is F = mv 2/r.

For a 72.5kg male, who must complete one rotation in order to land successfully, the main thing he can control is his radius by controlling the tightness of his tuck while rotating. A tighter tuck (smaller r) increases the force, allowing him to rotate faster. Using v=rw, estimating a very tight tuck of 2.5ft in diameter (r=.381m), we can approximate that the Force of rotation is mrω 2, or (72.5*.381*π2)=272.6N

The wall run – (http://www.youtube.com/watch?v=2OR6yon8VpQ)

The wall run is used to scale high walls by planting one’s foot and pushing against the wall. Thinking logically, we’ll get a different outcome if the force applied against the wall is at varying angles. If we push directly into the wall, the normal force will counter our force applied, and we will move only horizontally away from the wall, which won’t help us reach the top of the wall. Similarly, if our force applied is only vertical, we will just slip down the surface of the wall and fall down. The optimal angle that gives us both upward movement and prevents us from crashing face-first into the wall is 45 degrees.

This becomes a simple force problem to understand. To not crash into the wall, our Force applied in the x (Fa cos (45)) is equal to the normal force. Furthermore, the forces in the y direction are the force of friction opposing our downward applied force (and so is up), the force applied (Fa sin 45), and the force of gravity caused by our weight. Summing the forces:

Fa cos 45 = Fn

Ffr – Fg – Fa sin 45 = ma

(there is only acceleration in the y)

Plugging in,

µFa cos 45 – mg – Fa sin 45 = m a.
Estimating a coefficient of friction of .8 (we wear very grippy shoes), m = 72.5kg, and a final acceleration of positive 3 m/s2

One last simplification gives us

Fa = m(a+g) / (µcos 45 – sin 45). Using the estimations, we require a Fa of -2153N (down and into the wall) to give us an upward acceleration of 3 m/s2.

In the end, by looking at some physics equations, we can use our intuition and a few calculations to better traverse our environment in a more efficient way by using optimal angles, and tighter tucks in our rotations.

Portals in Ocean and Sky

Portals in Ocean and Sky

The video game Portals is centered around the use of the Aperture Science Handheld Portal Device, or portal gun. The gun can fire projectiles that upon impact on a flat surface expand into either an orange or a blue portal. By entering one portal, the player can exit from the other.

For this blog post, I am taking inspiration from two other weeks. In this post, I will be looking at the flow rate of water if the portal gun created a portal at the bottom of the Mariana Trench and then, taking a flight up to the stratosphere like Felix Baumgartner did with Red Bull, fired another portal onto the balloon.

Intuitively, we know that the pressure at that height is very low whereas the pressure at that depth is very large. Thus, the water should flow from the trench portal out of the stratosphere portal.

To understand this, we will use Poiseuille's equation.

Since the portals make it so that a path from the ocean to the sky is not a straight line from a to b the idea of height, y, is made strange. One idea is that the portal is worm-hole-like. The two portals may be connected by an infinitesimally small tunnel of near zero length L.  So, the flow rate would be infinite. For the sake of argument, let us assume the tunnel is 10^-6 m long.

The portal can accommodate a young woman and have about 2 feet in height left. The average height of a 20+ American femaile is 5 ft 4 in according to Wikipedia. We will assume the portal can be approximated as a circle (it's really an ellipse) and use 1.9 meters as the diameter. The radius shall be 0.95 meters. The viscosity of water near 0 degrees Celsius will be 1.8*10^-3 Pa*s.

The Mariana Trench has a pressure of about 1086 bars, or 108,600,000 Pa according to Wikipedia. The pressure at that height is very low and we shall assume it is zero.Setting up the equation,

The resultant answer is 6.8 x 10^16 m/s . This is overly large due to the portal's small length and our assumption that the flow is not turbulent. The volume flow rate is about 1.9 x 10^16 m^3.