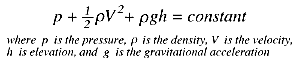The Physics of the Heart

As we are learning about fluids in motion, I started to wonder about the mechanism behind the pumping of the heart. The heart is made up of two different chambers: the two atria at the top of the heart and the two ventricles at the bottom of the heart. The heart beats by the contraction and relaxation of the heart muscle. To pump blood to the rest of the body, the heart muscle contracts the ventricle chambers causing the area to decrease.

Bernoulli's Equation

Due to the equation of continuity, we know that if the area decreases, the final velocity must increase and, therefore, the blood rushes from the heart to the rest of the body. Additionally, as the area decreases the pressure increases as shown by Bernoulli’s equation. This would force the blood to rush to regions of lower pressure, as fluids in motion flow from high pressure to lower pressure.

Finally, when the heart muscle relaxes, it increases the area of the atria chambers and, therefore, decreases the pressure, and the blood flows back to the heart to be re-oxygenated and cycled back out throughout the body again.

Physics in Gymnastics

            I used to love the show Make it or Break it, which follows the lives of a few gymnasts. I was always impressed by the moves and jumps that the gymnasts were able to do. I found the vault to be one of the most impressive events. In the video above, one of the characters from the show, Kaylie, preforms the vault. To perform a vault, a gymnast begins by running down a runway, which is usually padded or carpeted. Then, they jump onto a springboard and spring onto the vault with their hands. In the video, Kaylie is doing a vault from the Yurchenko family, in which a gymnast puts their hands onto a mat that is placed before the springboard, does a round-off onto the board and then does a back handspring onto the vault. After springing onto the vault, the gymnast proceeds with their off-flight, which can be as simple as leaping over the vault or as complicated as doing several twists and turns in the air. The gymnast then lands on a mat on the other side of the vault. 

According to Newton’s second law, the more mass and acceleration a gymnast has when running towards the vault, the greater the force they exert on the springboard will be. Gymnasts must reach a maximum velocity while running to the springboard in order to produce a maximum force. If we assume that Kaylie’s mass is 45 kg and that she is running to the spring board with a velocity of 4 m/s over a period of 5 seconds, what would the force that she exerts be?

F=ma

F=m(v/t)

F=(45 kg)((4 m/s)/(5 s))

F=36 N

Newton’s third law states that for every action, there is an equal but opposite reaction. Therefore, when a gymnast jumps on a springboard, she exerts a force on the springboard, which exerts an equal force back on the gymnast, which then propels her into the air. The angle at which the gymnast hits the springboard is very important because the more vertical the angle is, the greater the force will be to propel the gymnast higher into the air. Let’s say that Kaylie jumps onto the springboard at an angle of 80 degrees, which is not completely vertical. What would the new force that she is exerting be?

F_f = F_i sin Θ

F_f = (36 N)sin(80^o)

F_f = 35.45 N (less than the original force of 36 N)

  

When a gymnast then pushes off the vault, her hands exert a downward force on the vault and the vault exerts an equal force on her. Due to the conservation of momentum, gymnasts cannot gain any angular momentum once they spring off the vault. The greater the angular momentum, the more potential the gymnast has for doing flips in the air. Gymnasts can gain angular momentum by pushing off from the vault at an angle. Once they are in the air, gymnasts often curl into a tight ball to achieve more flips because the smaller their radius, the faster they spin. When they are about to land, gymnasts then extend their bodies because that slows down their rotational speed, which ensures that they will land smoothly on their feet.

We can calculate the initial energy that a gymnast has during her run to the vault, which is the maximum energy she will have throughout the entire event. A gymnast's initial energy is kinetic energy. The greater the velocity is that the gymnast has while running, the greater the kinetic energy is that she will have to complete the rest of the vault. What is Kaylie’s kinetic energy at the beginning of her run?

            KE= ½ mv²

            KE= ½(45 kg)(4 m/s)²

            KE= 360 J

           After the run, the gymnast jumps onto the springboard and her kinetic energy is then transferred into the springs of the board as spring potential energy. Assuming that no energy is lost due to friction or air resistance, the potential energy would be the same as the kinetic energy. If we assume that the spring compresses 0.15 meters when Kaylie jumps onto the springboard, what would the spring constant be?

           PE_s= ½ kx²

           360 J= ½ k(0.15 m)²

           k= 32,000 N/m

As the gymnast pushes off the vault, the spring potential energy is then converted to kinetic energy and gravitational potential energy. As the gymnast flips through the air, her kinetic energy increases and her potential gravitational energy decreases. However, throughout the entire vault, energy is conserved.

The physics of hockey sticks

At the Flyers game last Monday night I noticed four hockey sticks break over the course of the game. This number seemed so high to me, so I decided to investigate. My boyfriend is an avid sports fan and he said that the sticks used to break less often because they were made of a different material in the past.

Image from NWSportsBeat.com

In the 1980s did aluminum hockey sticks became popular, but now composite sticks are the most popular. Since hockey sticks can bend up to 30 degrees, they can be modeled by equations for elasticity in solids. In a paper by Russell and Hunt (2009), they investigated the Young's modulus for different types of hockey sticks. The wood hockey sticks had the lowest Young's moduli (8.88 - 16.25 GPa), the composite sticks were in the middle (31 - 42 GPa), and the aluminum sticks had the greatest Young's moduli (52.62 GPa).

Hockey sticks are sold with a certain "flex" value that describes how much pressure a stick can take. The flex value means the "amount of force required to 'flex' the stick one inch" (Monkey Sports). The average flex is about 85, because it is recommended that players choose a flex value that is at least half the weight of the player. Since players put more weight on the stick during certain shots, like slap shots, the stick may break during a particularly powerful shot because of too much flex. It is interesting to think about hockey from a physics point of view because players, coaches, and manufacturers need to be aware of the physics of force and pressure in order to design good sticks.

Macy's Thanksgiving Day Parade Balloons

We just finished up with buoyancy, but are still talking about fluids, which I was thinking about while watching the Macy’s Thanksgiving Day Parade, and the physics of the parade balloons. The balloons would have a force of gravity pulling them down, and a force of buoyancy from the air pushing it up and allowing it to float (assuming it is a sunny and windless day). 

ΣF=ma=0=F_B-F_g

F_B=mg

ρVg=mg

The balloon (specifically the Big Bird balloon) is filled with 12,000 cubic feet of helium, which has a density of 0.164 kg/m3, making the balloon weigh about 2,000 N (ignoring the weight of the balloon). In this case, the balloon is not accelerating in the y direction, so the forces must equal zero, meaning that the buoyancy force must be equal to 2,000 N. In the x direction, there would be a forward force by the force of the humans pulling the balloon, and the drag force of the balloon.

ΣF=ma=F_pulling-F_D

ma=F_pulling-(½ρv²C_DA)

For this case, the drag would have to be a less force than the force of the people pulling the balloons, since the balloon should be accelerating forward. Assuming the drag coefficient is .47, the density of the air is 1.225 kg/m³,the balloon has a radius of 6.5 m, and the balloon is traveling at 1 m/s, the drag force would be 32.2 N. So, the force of the people would have to be above this, on a windless day. Adding wind would drive the system out of whack, which is why there are actually many issues with the Macy’s Thanksgiving Day Parade, as seen in this video!

When Shopping Could Kill

This year at Macy's,  Black "Friday" began at 6:00PM on Thanksgiving Day. I find this reprehensible. Someone has to work on Thanksgiving so that hundreds of thousands of people can race, climb over, and fight each other for the best savings. People have gotten hurt, even been killed by the rush of shoppers. My goal with this blogpost was to find a case study and look at the kinematics of such a huge crowd of people and the resultant risk of being shoved or trampled in the initial rush.

The example I found was Macy's Flagship store at Herald Square in NYC. According the ABC News, 15,000 people waited on line for the doors to open at 6:00 pm. (http://abcnews.go.com/Business/black-friday-off-roaring-start/story?id=35444641)

I decided to ask, if all 15,000 people sprinted into the store, what would their combined momentum be? Their kinetic energy? What would happen if this horde of people ran into a wall? What would happen to a person who fell under their feet and was trampled?

If the average mass was 75kg and each person ran at 6.7m/s (the average sprint velocity according to ask.com) their combined momentum would be:

p=mv

p=15,000*75kg*6.7m/s 

p = 7.54*10^6 kgm/s

Their kinetic energy would be:

KE=.5*m*v^2

KE=15,000*.5*75kg*(6.7m/s)^2 

KE = 2.53*10^7 J

If the crowd had to stop, for instance, if the front row hit a wall, how many people would be crushed? We'll assume everyone has rubber soled shoes on, and the floor is made of concrete, The coefficient of kinetic friction between rubber and concrete is .6-.85 according to Wikipedia. We will use .725 If everyone tries to stop by sliding on their feet, it will take:

KEf-KEi=Wnc=Fdcos()    

 cos()=-1      F=mg

-2.53*10^7 J = .725(15,000*75kg*9.81m/s^2)d

d=3.16m

If each person has a depth of .5m, this means that at least six rows of people will be crushed against the wall before the crowd comes to a halt. From the picture below, it looks as if each row coming down the hall is 15 people wide. That's 90 people. 

Of course, crowds don't really move like that, but I also did not take into account the greatest factor that would make the crowd take longer to slow down: the difficulty in communicating the need to stop. 

A more realistic situation: A single person falls. It has happened before. If, as we assumed before, the crowd is 15 people wide, it will be 1,000 people long. If the whole crowd stops as before, it will still take 3.16 m to stop the whole crowd, so the individual will already have been trampled by 6 people (if the crowd is very organized, that is). More likely, the crowd doesn't stop, and all 1,000 people run over the poor individual.

The moral? Black Friday is Very Scary and everyone should stay home.

Skiing and the Non-Conservative Force

Skiing and the Non-Conservative Force

With ski mountains around the country opening for the season, I began to think about the physics of skiing.   For a skier, we know that Energy at the top and bottom of the mountain is equal to the skier’s kinetic energy plus the potential energy:

E_tot = KE + PE

At the top of the mountain, the skier has no velocity, and only gravitational potential energy:

E_top =  (1/2)mv² + mgh = (1/2)m(0)² + mgh = mgh

At the bottom of the mountain, the skier has no kinetic energy or gravitational potential energy (if the height at the bottom is arbitrarily defined as 0.  So, the work done by the non-conservative forces between the top and the bottom of the mountain is equal to the gravitational potential energy at the summit:

W_NC = ∆KE + ∆PE = (0-0) + (0 – mgh) = -mgh

For my home mountain, Stratton Mountain in Stratton, Vermont, h (the vertical drop) is 611 m.  Therefore, the work done by the non-conservative force on a skier of mass 70 kg is equal to:

W_NC = mgh = (70 kg)(9.8 m/s²)(611 m) = 419,146 J

But where does all this energy go?  Most of it is lost to friction when the skier turns his/her edges into the snow to decelerate (some of it is also lost to air resistance).  This seemed like a lot of energy per skier, so I asked myself the question: if all of this energy were transferred to the snow, how much snow would each skier melt per run?  I assumed that the snow was already at its melting point, and used the enthalpy of fusion for water (334 J/g) to determine that each run by a 70 kg skier could melt 1.25 kg of snow. 

419,146 J x (1 gram snow/334 J) = 1254.9 g = 1.25 kg snow

If Stratton Mountain were operating at full capacity (33,428 skiers/hour), there would be a total of 4.2 x 10⁷ kg of snow melted per hour.  Thus, most of the energy from the non-conservative work must go elsewhere, and not directly to melting snow.

Volcano Physics

          For one of my other classes, we are studying the eruptive styles and general characteristics of volcanoes, specifically five in Southern Chile. I realized while looking them up that pretty simple physics could be applied to the eruptions. During the more explosive eruptions, material expelled from the volcano basically acts as a projectile, going straight up until the negative acceleration due to gravity causes it to stop its upward direction of motion. Since the height of the column of ash is usually recorded as an indicator of the explosivity, I decided to use this to determine the initial speed that the ash must be going as it passes the top rim of the volcano.

            On April 5^th, 2009, there was a relatively small eruption that created a column that reached 600 meters. Since we know the height, acceleration (due to gravity) and final speed, we can calculate a rough estimate for the initial speed of the erupted material (ignoring buoyancy from the heat that would increase the height reached and air resistance) using the equation:

v_f ²= v_o² + 2aΔx

(0 m/s)² = v₀² + 2(-9.8 m/s)(600 m)

v₀ = 108 m/s

            And that’s from a small eruption. Some eruptions can cause columns that are around 40 km high. So, fun PSA, this is why you really shouldn’t be near volcanoes while they’re erupting. They can cause a fairly alarming amount of damage.  You’d think it’s common knowledge, but it’s really not. People still climb erupting volcanoes all the time in unregulated areas.

(http://travelvista.net/5-deadliest-volcanoes)

Nevado del Ruiz eruption column, November 13^th, 1985

            I also thought it might be interesting to see how much work an eruption does to make the ash go so high. I couldn’t actually find the amount of erupted material for that eruption, but for a volcano in the same subduction zone, Nevado Del Ruiz (in Colombia), with a 35 km column, the erupted mass was 7.0 x 10⁸ kg. (This was an incredibly destructive eruption, by the way.)

W = mgh

W = (7.0 x 10⁸ kg)(9.8 m/s²)(3500m)

W = 2.4 x 10¹³ J

 Which is, unsurprisingly, quite a large amount of energy.