At the time I came to the realization that physics exists as a field of study, I was probably around 5 years old and watching a Disney movie titled, Ice Princess (2005). In the movie, Casey is a teenage #womaninSTEM, who is tormented by the decision she needed to make in choosing between her passion and her education. The movie makes a point of highlighting Casey’s good grades and physics knowledge and how her mother really wants her to apply to Harvard. However, Casey was an angsty goody two-shoes, who also was good at figure skating, and for some reason could not both apply to Harvard and pursue figure skating. My physics-related memory of the movie is Casey speaking with her physics teacher and someone writing down physics formulas and free body diagrams on the chalkboard, which were then overlaid with videos of figure skating. I had solidly forgotten about the relationship between physics and figure skating and that movie for a good 15 years until I had the pleasure of being an object of collision several nights ago at an open skating event in the 1964 Arena. I had also really thought the main character was played by Anne Hathaway until I researched the movie for this article, which is disappointing finding to say the least.
Although object #1 in the collision profusely apologized for skating into me while attempting to skate backwards without a rear view camera, I sincerely thanked object #1 for giving me a topic idea for my physics article on the relevance of physics in real life events. I plan to use this article to discuss how the skating collision relates to physics through the impulse and the conservation of momentum and energy, in addition to discussing the physics that makes ice skating possible. The collision began with I, object #2, skating at a very slow speed with my friend, who was dressed as a life-sized Hanukkah dreidel. Then, I felt something make contact with my back and push me forward slightly, watching as the other skater, object #1, moved at an angle away from me, at a decreased speed and angle of trajectory than I had initially seen them skating at. I am going to attempt to visually depict the event below. If the diagram is not adequate, please feel free to email me and we can recreate the scene at the next open skate event. I am not joking.
Summary of Collision Events
Before Collision
Object #1 initially moving at velocity greater than object #2.
Object #1 initial velocity direction was at an angle to the x-axis, assuming the axis is located in the direction of motion of object #2.
Object #2 initial velocity near 0 m/s in direction perpendicular to the y-axis, at a 0° angle overlaying the x-axis.
After Collision
Object #1 moved with a slightly decreased magnitude of velocity, at an angle greater than the initial angle of velocity.
Object #2 moved in the same angle as its initial velocity, with a magnitude of velocity greater than the initial.
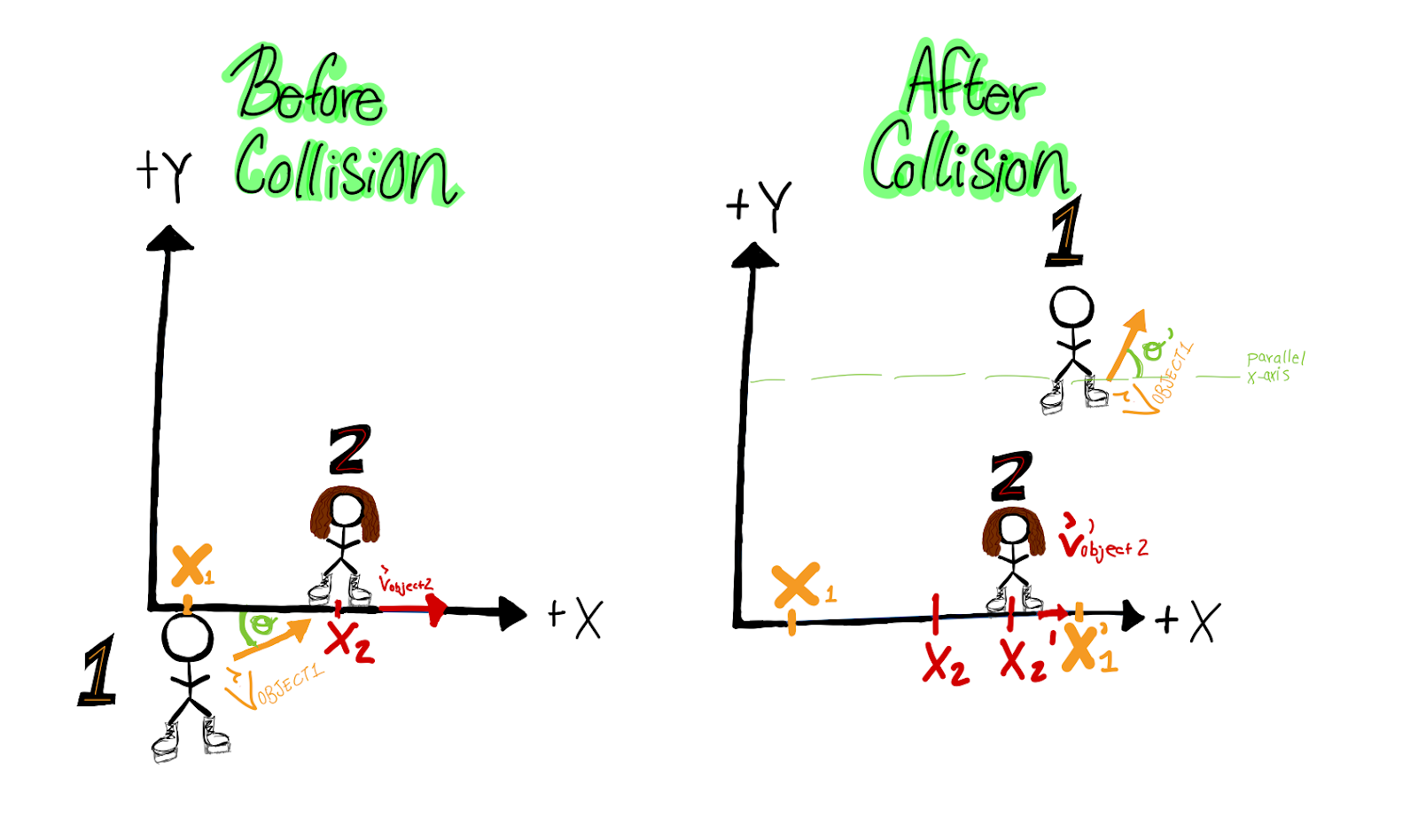
Figure 1. Diagram of collision. Figure represents position and change in direction of velocity before and after collision event by the two skaters. The initial velocity of object #1, labeled above, is of greater magnitude than that of object #2, and decreases after collision. The initial magnitude of velocity of object #2 is low, but increases after collision with object #1. The x-axis is overlaid with the direction of velocity of object #2, while the direction of velocity of object 1 is represented by the orange velocity arrows, accompanied by a green indication of angle. Initial and final velocities and positions are represented by the labels, " v " and " v’ ", respectively, with object #1 being orange, and object #2 being red. My apologies if you are color blind. The same color scheme follows for position, as is indicated on the x-axis with initial position being “ x ” and final position being represented at “ x ‘ “.
Impulse and Conservation of Momentum
Momentum | Conservation of Momentum for Elastic Collisions | Impulse |
p = mv | Δp = 0 p0 = p’ m1v1sinθ1+ m2v2sinθ2= m1v1’sin θ1’+ m2v2’sin θ2’ | I=Δp I = FAvgΔt |
In an elastic collision, with no external forces applied, both energy and momentum are conserved as objects bounce off of each other. Our collision was likely elastic because we did not continue to move together at a new shared velocity after the collision, but object #1 was deflected away from me, object #2, because the initial velocity of object #1 was at an angle compared to my direction of velocity. I was pushed forward slightly due to the force applied to object #2 by object #1 upon impact. The inverse relationship between average force (FAvg) and change in time (Δt) can be seen in the formula for impact (I): I = FAvgΔt. Additionally, because we were ice skating, there is external force from friction interfering with the possibility of a perfectly elastic collision, but very little, as the coefficient of friction between ice skates and ice is between 0.006 and 0.016 (Lozowski et al., 2013). For comparison, a surface considered to be slip-resistant has a coefficient of friction ranging from 0.2 to 0.29 (Mohamed et al., 2011).
The force exerted on object #1 when colliding with object #2 was small enough to allow object #1 to continue motion at a different angle with only a magnitude of velocity slightly less than than object #1’s initial velocity. The small amount of force applied to object #2 during the collision was likely prolonged by the cushioning in the puffer jacket on object #1, and the hoodie on object #2, resulting in a decreased magnitude of force of impact in the collision (FAvg), due to an increase in change in time (Δt) during contact. In addition, the angle of approach of object 1 was altered because collision with object 2 interfered with the path of object 1.
Conservation of Energy
Conservation of Energy |
ΔKE0 + ΔPE0 + WNC = ΔKE’ + ΔPE’ KE = 1/2mv2 |
Object #1 initially had greater kinetic energy before the collision than they did after the collision. Some of their kinetic energy was transferred to object #2 upon collision, where it was absorbed by the cushioning of clothing, or transferred to object #2 as potential energy, and immediately translated into a short increase in the magnitude of object #2’s velocity, while object #1 experienced a slight decrease in magnitude of velocity. Non-conservative work would have a small value on the part of friction, as ice has a very low coefficient of friction, as mentioned earlier. It is likely that the mass of object #2 was greater than object #1 because of the minimal change in position experienced by object #2 as compared to object #1. However, the mass and speed of each object are unknown, so cannot be used to calculate KE or momentum at this time.
How Physics Allows For Ice Skating

Figure 2. Physics of ice skating. Figure originally published at (Physics of Ice Skating), https://www.real-world-physics-problems.com/physics-of-ice-skating.html. The figure presents the direction of the force vector as at an angle less than 90° to the direction of motion, although it is perpendicular to the direction the skate is facing. The angle of the skate from the direction of motion is represented by “a”, as this angle contributes to the acceleration that may be obtained, and the force vector is represented by “F”.
Ice has a low coefficient of friction in contact with ice skates because there is a layer of liquid water on top of the ice, which reduces the force of friction between the ice and the blade of the skate. In addition, the metal blade is a great conductor of heat, so that any friction that does result from skating generates heat which melts the ice into liquid, allowing for ease of skating. You can brake or speed up when ice skating due to the force applied from the edge of the blade on the ice in a perpendicular direction, allowing for the skater to push off of the ice and accelerate. Often, people skate with the hind leg pushing off of the ice to form enough friction to accelerate, and then switch to the other leg and do the same. Skaters have the option to increase the angle between the blade and where it is in perpendicular contact with the ice, providing even greater potential for acceleration (Physics of Ice Skating).
References
Cabot, M., & Davis, H. (2005). Ice Princess [Film]. Walt Disney Pictures.
Lozowski, E., Szilder, K., & Maw, S. (2013). A model of ice friction for a speed skate blade. Sports Engineering, 16(4), 239–253.
Mohamed, M.K. & Samy, Abdelhalim & Ali, W.Y. (2011). Friction Coefficient of Rubber Shoe Soles Sliding Against Ceramic Flooring. KGK Kautschuk Gummi Kunststoffe, 64, 44-49.
Physics of ice skating. Real World Physics Problems. From https://www.real-world-physics-problems.com/physics-of-ice-skating.html




![Animated] Spinning Desk Chair | Chair, Desk chair, Animation](https://i.pinimg.com/originals/2f/64/e8/2f64e84182323bd7d062f2ff2f981c68.gif)








