The Swan Lake is my all-time favorite ballet. You never get tired of it, at least not after seeing it every winter for eighteen years nonstop. One of the many reasons why it is considered an absolute masterpiece is that it is full of extremely challenging techniques, such as the 32 fouettés in the Black Swan pas de deux https://youtu.be/XfmSv0z205s (0:37).
I found out, only recently, that the physics of fouetté is actually pretty neat. At the very start of the unstoppable motion of “whipping” around (the origin of the name “fouetté” in French), the ballerina pushes off with her foot en pointe to generate a torque. However, as she starts to turn, the friction between her pointe shoes and the floor as well as that between her rotating body and air generates a small opposing torque that reduces her angular momentum according to the equation:
Ignoring the friction, we would observe the conservation of angular momentum in each turn:
In the case where friction is not to be ignored, we might wonder how the ballerina maintains her rotations (in fact, for 32 times), since friction would eventually wind her down. The secret lies in the momentary pause when she faces the audience between each turn. Her supporting foot flattens and then pushes off the floor just as she has done the previous turn. As she twists and rises back en pointe, a small amount of new torque is generated.
Meanwhile, her arms extend from the first position into the second, helping her to maintain balance. The 32 fouettés look as beautiful and seamless as they do because her center of gravity remains directly above the area of contact with the floor at all times. As you can imagine, balancing is significantly harder when the area of contact is as small as the tip of a pointe shoe. With endless practice, a skilled ballerina will be able to keep her center of gravity constant by maintaining a strictly vertical rotational axis – an upright back and tightened core.
At the same time, her other leg never stops moving. During the short pause, the motor leg extends from the passé position and moves from the front to the side before it folds back to passé again. By staying in motion, the motor leg is storing some of the momentum of the turn. When she kicks the leg out to the front and side, some momentum is transferred to the moving leg; and when she folds the leg back in, the momentum gets transferred back to the body, propelling her around as she goes back en pointe. The momentum, thus, travels back and forth between her leg and body, keeping her in motion.
The motion of the elevated leg also helps explain why we perceive a pause, or rather, the slowing down of her rotating motion. According to the equation of the moment of inertia,
When she extends the leg from passé, r is increased, so her moment of inertia is increased, and if we assume that the angular momentum is conserved before and after the extension, her angular velocity must be reduced, resulting in the “pause”. Similarly, when she folds the leg back into passé as she starts a new fouetté, r is reduced, so her moment of inertia is reduced, therefore the angular velocity must increase, which is why we perceive that she speeds up as she starts to turn.
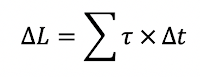




No comments:
Post a Comment
Note: Only a member of this blog may post a comment.