Physics of tennis at it's best

While watching a recent tennis tournament, I noticed that the serves' speeds were being measured in km/h (it took place in Geneva). Thanks to all the recent kinematic work we've been doing I immediately thought "Ok gotta convert km/h to m/s). Obviously I didn't, but that initial thought got me thinking about how the phsyics we've been learning can by applied to this situaition. Specifically, I was watching American John Isner, who at 6'10" has one of the fastest serves of the game. Novak Djokovic is considered to be the greatest of all time at returning serve. So I got to thinking, how much goes into the serve, and similarly what must the returner do to respond? The last time Isner and Djokovic played each other was in 2018 at the Nitto ATP finals in London. As shown in the clip above, Isner served to the corner of the serve box with a speed of 130 mph. Using our understanding of momentum and impulse, the first question was with what force is Isner hitting the ball?

Vo = 0 m/s
Vf = 130 mi/h = 58.12 m/s
mass of an average tennis ball = 59.4 g = 0.0594 kg
time of impact = 4ms = 0.004s
Change in momentum = F(change in time)
mv = Ft
(0.0594 kg)(58.12 m/s) = F (0.004s)
F = 863 N

My next question was with what velocity will the ball hit the ground? At what angle? To answer this I used kinematics. First, I made sure that the speedometer used measured the velocity of the ball right after it is hit, and not as is passes over the net. Using the height at which Isner usually hits his serves, and the distance the ball would travel to land in the right hand corner of the service box, I calculated the velocity with which the ball hits the ground.
 
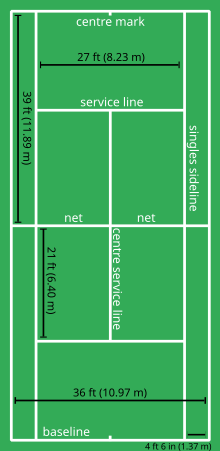
Isner serves the ball at the center mark on the baseline. Assuming the ball travels in a straight line from the contact point to bottom right corner of the opposite service box, I used two triangles to find that distance traveled.
c = 18.74   z = 19.04 m

The estimated force of air resistance against a tennis serve is 0.00114*v^2 so 3.85 N. We also have to consider the force of gravity acting on the serve, which would contribute a force equal to mgsin(theta). Theta would be equal to tan-1(18.74/3.4) = 79 degrees. Thus, gravity would contribute (0.0594 kg)(9.8 m/s^2)(sin(79)) = 0.573 N.

Using F=ma we can determine the deceleration of the ball over the course of the serve.

-3.28 N = (0.0594 kg) a

a = -55.17 m/s^2

Then using this acceleration, and our adjusted coordinate system, we can determine how fast the ball was going when it hit the ground.

Vo = 58.12 m/s

a = -55.17 m/s

x = 19.04 m

Vf?

Vf^2 = (58.12)^2 + 2(-55.17)(19.04)

Vf = 35.17 m/s

The ball bounces at the service line and then continues it's trajectory towards Djokovic. Assuming conservation of momentum, and that the time of the bounce is negligible, we can say that the velocity of the ball after the bounce is the same as it was before the bounce. When hitting the return, Djokovic was about two feet behind the baseline (I'm estimating) and hit the ball near his shoulders/head. Djokovic is 6'2", and so the estimated height the ball reached would be 5'8"(?) or about 1.7272 m. All this can be used in a similar way as before to figure out how much more distance the ball traveled post bounce, which would be about 6.47 m. 

Now one of the most impressive aspects about tennis is the speed of the game, and more specifically how fast players have to react to return serves such as this one. Thus, I wanted to calculate exactly (roughly) how long Djokovic had between the serve and the return to react. I would break this up into two components, one for the pre-bounce and one for the post-bounce, because after the bounce the 

deceleration of the ball would be different since gravity would now be acting against the motion. 

Pre-bounce:

Vo = 58.12 m/s

a = -55.17 m/s

x = 19.04

t?

19.04 = (58.12)(t) + 1/2(-55.17)t^2

0 = -19.04 + 58.12t - 27.585t^2

t = 0.4 sec

Post-bounce:

a =( (-3.85) + (-.573) ) / 0.0594

a = -74.46 m/s^2

Vo = 35.17 m/s

a = -74.46 m/s 

x = 6.47m

6.47 = 35.17t + 1/2(-74.46)(t^2)

0 = -6.47 + 35.17t - 37.23t^2

t = 0.25s

Therefore, Djokovic had about 0.65 seconds to react to the serve and hit a return. Very impressive.

Another notable physics aspect of tennis is the way in which players get the ball. They often try to hit the ball with topspin for most of their shots. I began thinking about this recently in the context of our angular kinematics unit. Growing up I always understood the use of top spin as a way to keep the ball from going too high up in the air, that is you want to keep your shots just barely passing over the net. This would make sense as the higher up the ball goes, the longer your opponent will have to react and get prepared to make a better shot. I have also been thinking about it in terms of energy, in that it requires more energy to return the ball at a comparable speed but also adding in a rotational component. Top spin generally keeps the ball lower to the ground, making it less likely to fall comfortably in your opponents strike zone. Apparently this has something to do with a Magnus force.

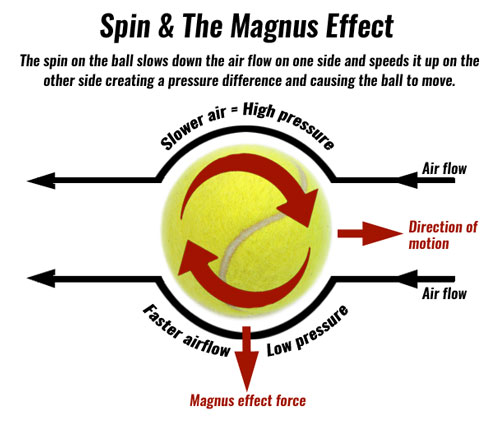
Often when I watch matches they talk a lot about how the weather conditions impact the play, such as the ball moves faster, or they say the court plays faster, on hotter days. Indoor courts play different than outdoor courts, and the game can be played on clay, grass, or hard court which all have their own effects on the ball as well. Players have to take all of this into account whenever they step onto the court, making my appreciation for what they can do (...and what I sorta used to do in HS) that much greater.

 

In case you were wondering, Djokovic won that match 6-4, 6-3 and leads their head-to-head 10-2.